Свойства касательной.
1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ( AB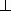 
OK, рис.40 ) .
OK, рис.40 ) .
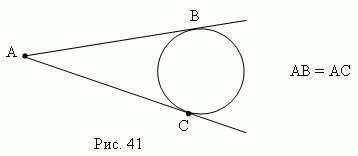
2) Из точки, лежащей вне круга, можно провести две касательные к одной и той же окружности; их отрезки равны ( рис.41 ).
Терема о вписанном угле в окружность.
Теорема: вписанный в окружность угол равен половие градусной меры дуги, на которую он опирается (или половине центрального угла, соответствующего данной дуге), то есть 
.
Свойство угла, опирающегося на диаметр.
Теорема: вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.
AC-диаметр 
Cвойство отрезков касательных. Окружность, вписанная в угол.
Теорема 1: если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть PB=PC.
Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть PO-биссектриса.
Свойство отрезков хорд при внутреннем пересечении секущих.
Теорема 1: произведение отрезков одной хорды равно произведению отрезков другой хорды, то есть
= 
.
Теорема 2: угол между хордами равен полусумме дуг, которые этими хордами образуются на окружности, то есть
Теорема: вписанный угол в окружность опирается на диаметр тогда и только тогда, когда он прямой.
AC-диаметр
Теорема 1: если из одной точки, не лежащей на окружности, проведены к ней две касательные, то их отрезки равны, то есть PB=PC.
Теорема 2: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть PO-биссектриса.
Свойство отрезков хорд при внутреннем пересечении секущих.
Теорема 1: произведение отрезков одной хорды равно произведению отрезков другой хорды, то есть
Теорема 1: произведение отрезков одной хорды равно произведению отрезков другой хорды, то есть = .Теорема 2: угол между хордами равен полусумме дуг, которые этими хордами образуются на окружности, то есть
Комментариев нет:
Отправить комментарий